MT Generadora Multicinta

Formato de Entrada : BQ₀0ⁿB

Formato de Salida : Baⁿb²ⁿaⁿB

Q0 : Posición inicial; recorremos la 1º cinta escribiendo en la 2º tantas a’s como simbolos (representamos n como el numero de 0’s) tenga la 1º cinta (aⁿ).

Q1 y Q2 : Recorremos el cabezal de vuelta y escribiendo en la 2º cinta b’s al doble de velocidad que avanzamos por la 1º cadena (b²ⁿ).

Q3 : Recorremos por última vez la 1º cinta y escribimos el último tramo de a’s en la 2º cinta (aⁿ).

Q4 : Estado final.

Nota :

1º cinta : El numero de 0’s nos indicará el valor de n.

2º cinta : Cinta de salida.

MT Comprobadora de Secuencia Creciente Modificada

Formato de Entrada : BQ₀Q00^N10^M10^P…10^ZB

Formato de Salida : B0..0B

Q0 : Posicionamos un cabezal al inicio de la cadena y el siguiente después del separador.

Q1 : Vamos recorriendo la cadena comprobando si la parte que recorre el 2º cabezal es mayor que la que recorre el 1º cabezal.

Q2 : Estado final.

Seleccionamos una maquina multicabezal puesto que para la idea que teníamos para resolver el problema era la que mejor se acoplaba al diseño anterior.

Nota : igual que el anterior comprobará si la cadena es mayor estricta.

MT Comprobadora de Secuencia Creciente

Formato de Entrada : BQ₀0^N10^M10^P…10^ZB

Formato de Salida : B0..0B

Q0 : Estado inicial y eliminamos el 1º elemento.

Q1 : Vamos en busca del separador o blanco (final de la cadena).

Q2 : Marcamos símbolos del segundo término.

Q3 : Retrocedemos hasta el principio.

Q4 : Una vez hemos acabado la 1º sección comprobamos si el siguiente es mayor (ver notas).

Q5 : Desmarcamos las X.

Q6 : Estado final

Resumen:

Básicamente la forma de operar del autómata sería la de ir eliminando los elementos en una primera sección e ir marcando-los en una 2º sección(después del separador); una vez acabados los elementos de la 1º comprobaría si en la segunda todavía quedan elementos y si es así (en este caso es mayor que la anterior) volvería a empezar considerando la 2º sección como la inicial; es decir trabajaría a pares de secciones 1-2,2-3,3-4… y así hasta el final.

Notas :

Esta MT comprueba si dada una cadena de caracteres con el formato de entrada los diferentes grupos de 0’s tienen orden creciente estrictamente; es decir 0n<0m<0p…<0z>

MT Multicinta que Cuenta Bloques de Ceros (0+1)*

MT Multicinta que Cuenta Bloques de Ceros (0+1)^*

Entrada: ...B0001001001000100B...

Salida: ...B00000B...

	{ 0, B }	{ 1, B }	{ B, B }
Q0	( Q0, {B, R}, {B, Z} )	( Q0, {B, R}, {0, R} )	(Q1, {B, Z}, {0, Z} )
Q1

Q0: Inicio de programa e inicio de la finalización del programa.

En este estado Q0 iremos borrando 0’s y 1’s mientras vayamos consumiendo símbolos de la cadena de entrada. En el momento en que se localice el símbolo 1, se procederá a escribir un 0 en la cinta de salida y, cuando se localice el símbolo B en la cinta de entrada, se procederá a escribir el último 0 en la cinta de salida.

Q1: Estado Final. Finalizar programa.

NOTA:

Hemos elegido esta MT Modificada porque nos permite realizar las operaciones con mayor rapidez y facilidad para hacer los cálculos, ya que tenemos la información en la primera cinta de entrada y escribiremos el resultado en la segunda cinta de salida.

Como sabemos, el poder computacional es ambas Máquinas de Turing es la misma.

MT Clásica que Cuenta Bloques de Ceros (0+1)*

MT Clásica que Cuenta Bloques de Ceros (0+1)^*

Entrada: ...B0001001001000100B...

Salida: ...B00000B...

	0	1	B
Q0	Q0, B, R	Q1, B, R	Q5, B, R
Q1	Q1, 0, R	Q1, 1, R	Q2, B, R
Q2	Q2, 0, R		Q3, 0, L
Q3	Q3, 0, L		Q4, B, L
Q4	Q4, 0, L	Q4, 1, L	Q0, B, R
Q5	Q5, 0, R		Q6, 0, L
Q6

Q0: Inicio de programa e inicio de la finalización del programa.

En este estado Q0 iremos borrando 0’s y 1’s mientras vayamos consumiendo símbolos de la cadena de entrada. Cuando se localice el símbolo 1, iremos a escribir un 0 en el bloque de resultado y, si se localiza el símbolo B, se procederá a escribir el último 0 al bloque de resultado final.

Q1: Buscar B para localizar el cabezal en el bloque de resultado.

Q2: Buscar B para escribir 0’s.

Q3: Retroceder hasta B para salir del bloque de resultado.

Q4: Retroceder hasta B para volver a iniciar el escaneo de 0’s y 1’s.

Q5: Escritura del último 0 en el bloque de resultado y nos vamos a finalizar el programa.

Q6: Estado Final. Finalizar programa.

Resumen Semanal 14-20 de Abril

El lunes por la tarde empezamos a hacer comprobaciones de las MT del grupo 11 para poder evaluar-les.
El jueves por la tarde continuamos con la evaluación (las trazas de la MT para caluclar los divisores suelen ser muy largas de realizar); tambíen comprobamos en parte nuestras MT y corregimos varios errores que se nos habian pasado por alto.

Resumen Semanal 7-13 de Abril

Ya que teniamos que realizar 2 MT, en primer momento nos dividimos el trabajo entre los 2 miembros del grupo.
El lunes realizamos una primera puesta en comun de lo que habiamos sacado, se corrigieron diversos fallos en las MT.
El jueves por la tarde nos reunimos nuevamente para comprobar ambas MT, hicimos diversas pruebas y parecen funcionar bien.
El viernes dejamos finalizadas las MT y las dejamos preparadas para poder publicar-las.

MT Divisores con 1 Cinta

Entrada : B0nB
Salida : B(0div1)1(0div2)1…1(0)1B

MT Estándar para calcular los Divisores de un Número N V2

Entrada: …B_q0000000000B…

Salida: …B0000$000000000$000101B…

	0	1	B	X	Y	$
Q0	Q1, X, R		Q5, $, L	Q0, X, R
Q1	Q2, X, L		Q5, $, L
Q2			Q3, $, L	Q2, X, L		Q3, $, L
Q3	Q3, 0, L		Q4, 0, R
Q4	Q4, 0, R					Q0, $, R
Q5				Q5, 0, L		Q6, $, L
Q6	Q7, 0, L		Q25, B, R
Q7	Q7, 0, L		Q8, B, R
Q8	Q9, X, R					Q13, $, L
Q9	Q9, 0, R					Q10, $, R
Q10	Q11, Y, R				Q10, Y, R
Q11	Q12, 0, L					Q14, $, L
Q12	Q12, 0, L			Q8, X, R	Q12, Y, L	Q12, $, L
Q13			Q8, B, R	Q13, 0, L
Q14	Q15, 0, L			Q18, 0, L	Q14, 0, L	Q14, $, L
Q15			Q16, B, R	Q15, 0, L
Q16	Q17, B, R
Q17	Q17, 0, L		Q8, B, R			Q25, $, L
Q18			Q19, B, R	Q18, 0, L
Q19	Q20, X, R					Q22, $, R
Q20	Q20, 0, R	Q20, 1, R	Q21, 0, L			Q20, $, R
Q21	Q21, 0, L	Q21, 1, L		Q19, X, R		Q21, $, L
Q22	Q22, 0, R	Q22, 1, R	Q23, 1, L			Q22, $, R
Q23	Q23, 0, L	Q23, 1, L		Q24, X, R		Q23, $, L
Q24						Q15, $, L
Q25

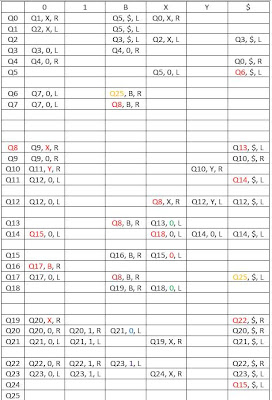
Q0: Inicio de programa y control del bucle de división por 2.

Entre este estado Q0 y Q4 se procederá a calcular el número N/2 del número de la cadena de entrada y se escribirá ese resultado a la izquierda del número dado.

En el estado Q0 se hace la primera marca X y control de salida del bucle ( Q5 ), reemplazando el símbolo B por $ con el fin de usarlo de separador entre el número N y bloque de resultados de los divisores de N.

Q1: Pone la segunda marca X.

Q2: Reemplaza el símbolo B por $ la primera vez que se pasa por aquí con el fin de utilizarlo como separador entre el número N y el bloque de N/2.

Q3: Escribir 0 donde haya B en el bloque de N/2 por cada iteración.

Q4: Volver al inicio del bucle.

Q5: Borra las marcas X dejándolas a 0.

Q6: Salir de la aplicación si no hay al menos un cero para evitar la “división por cero”.

Q7: Como mínimo habrá un cero y empezamos la comprobación de los divisores de N.

Q8: Inicio del bucle del cálculo de los divisores del número N.

Entre este estado Q8 y Q14 se hace la comprobación de los números que son divisores del número en la cadena de entrada.

En Q8 se controla el marcaje de X, es decir, si no hay más X volveremos a empezar el marcaje de las parejas Y.

En Q11 se controla el marcaje de Y, es decir, si no hay más Y entonces procederos a verificar si el número en cuestión es divisor del número N.

Q9: Buscar la marca $.

Q10: Marcamos con 0 con Y.

Q11: Comprobamos si hay más Y.

Q12: Retroceder hasta encontrar la marca X.

Q13: Se desmarcan las X y se vuelve a empezar con el proceso.

Q14: Se decide si el número realmente es un divisor de N ( Q18 ) ó no lo es ( Q15 ).

Q15: El número no era un divisor de N porque se encontró al menos un cero.

Q16: Decrementar en una unidad a N/2. El objetivo es eliminar todos los ceros.

Q17: Controla el final del programa ó la continuación con el cálculo de los divisores de N.

Q18: El número es un divisor de N porque se encontró al menos un X.

Q19: Iniciar la copia del divisor de N y control del final del proceso de copia ( Q22 ).

Entre este estado Q19 y Q21 se procederá copiar el número divisor de de N en el bloque de resultados, a la derecha del número dado.

Q20: Reemplazar B con 0.

Q21: Buscar X para volver a iniciar el marcaje ( Q19 ) .

Q22: Buscar el símbolo B y poner la marca de separación ( 1 ).

Q23: Buscar X en el bloque de números divisores ( N/2 ).

Q24: Volver a comprobar si aún quedan números en el bloque de N/2 ( Q15 ).

Q25: Estado Final. Finalizar programa.